Background #
Coordenadas baricéntricas #
Las coordenadas baricéntricas son coordenadas dentro de un triángulo o n-simplex (en varias dimensiones), estas coordenadas nos permiten parametrizar puntos dentro de un triángulo por lo que una coordenada baricéntrica en un triángulo equilátero en un punto P tendrá su compañero P’ en un triángulo rectángulo.
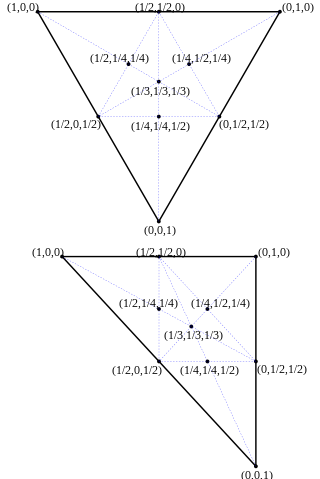
Uno de los usos de las coordenadas baricéntricas es el despliegue gráfico, en el cual se decide qué píxeles del dispositivo deben ser activados, para representar la primitiva (Rasterización), convertir un objeto continuo en coordenadas de mundo a un objeto discreto en el computador para su visualización.
El concepto de coordenadas baricéntricas data de 1827 introducido por el profesor alemán llamado Augusto F. Möbius, con las coordenadas baricéntricas podemos determinar si un punto está dentro de un triángulo, con esta informacion podemos colorear solos los puntos que esten dentro del triangulo o que la $\alpha ,\beta ,\gamma \in [0,1]$

Raycasting #
El raycasting es una herramienta que nos permite realizar ciertas acciones en lo que respecta a la geometría computacional y por obviedad los gráficos computacionales para modelar y renderizar objetos en 3 dimensiones 🎲 en una pantalla de 2 dimensiones. 🖼️
Para ello tenemos que pensar en cómo podemos ver las cosas a nuestro al rededor.

Cuando vemos un objeto lo que estamos viendo es la luz rebotar en el objeto en dirección de nuestro ojo. Sin embargo en nuestro caso es al revés: ahora desde nuestro punto de vista lanzamos rayos hacia direcciones específicas (esto se puede definir por la cantidad de rayos que queremos enviar y el tamaño del campo de visión) y revisar si estamos chocando contra algún obstáculo. De esta forma entonces podemos realizar un “escáneo” de nuestro alrededor y entonces renderizar el objeto en cuestión.
Pero, ¿entonces cómo logramos que ese objeto en 3 dimensiones se represente en un plano de 2 dimensiones? Bueno aquí es donde entra la función del plano de perspectiva. Cuando hacemos proyección en perspectiva lo que estamos haciendo es basicamente usar esta construcción geométrica para proyectar todos los puntos del modelo 3D en el plano de vista, para formar así un modelo 2D de la imagen. Es importante que el plano de vista sea paralelo al plano x-y de igual forma que el modelo que queremos dibujar.

Vale, ¿pero cómo entonces ya explicitamente? ok, voy con la explicación: Cuando definimos el plano de vista le vamos a definir en tamaño a lo ancho (x), por ejemplo si decimos que el tamaño es 100, entonces lo que veremos son 100 filas de pixeles de nuestra objeto, ahora nos falta el alto (y), y como ya sabemos que vamos a lanzar un rayo desde nuestro punto de vista hacia el objeto sabremos cuando choque y obtendremos la distancia real que tenemos hacia el objeto. Sin embargo esta distancia no es la que queremos saber ya que nosotros queremos la proyección en nuestro plano de vista, por lo tanto es necesario calcular la distancia “virtual”, vamos entonces a realizar el calculo de nuestro punto de vista hacia el plano de vista (d):

Con esta distancia hacia el plano de vista podemos entoncer obtener la proyección de la altura (y) de nuestro objeto. (la altura predeterminada es una constante que podemos variar para obtener diferentes alturas).
\[altura = \frac{alturaPred * distanciaVirtual}{distanciaReal}\]